艾略特波浪解說（第九回）關於斐波那契的解說

這次我們為大家解說關於艾略特波浪中的斐波那契數列。首先我們先確認一下什麼是斐波那契。

1 1 2 3 5 8 13 21 34 55 89 144 233 377 610・・・・・・・

如以上數列一樣有無限持續的整數數列。從1 1開始，2個相加的整數和是下一個數字的數列。

1+1=2 1+2=3 2+3=5 3+5=8 5+8=13・・・・・・

從以上計算式中也可以確認的到。這個數列就是被稱為斐波那契數列。有的網站把斐波那契數列稱為斐波那契級數，這是一個明顯的翻譯錯誤。「級數」是指把數列中的各項數字加起來的和，與數列的意思根本不同。也希望大家記好正確的用語。

在斐波那契數列中的各項整數被稱為斐波那契數字。如1 2 3 5 8 13 21 34 55 89 144等數字。另外，斐波那契數字之間的比例被稱為斐波那契比例。

下面我們用相鄰的大數除以小數看看。

例如：34÷21＝1.619047619・・・

144÷89＝1.617977528・・・

610÷377＝1.618037135・・・

如以上計算式一樣，結果大概都是1.618。



下面再反過來用小數除以大數看看。

21÷34＝0.617647058・・・

89÷144＝0.61805555・・・

377÷610＝0.618032786・・・

結果大概都是0.618。所以，1.618和0.618就是代表性的斐波那契比例。



另外，下面是中間跳過1個數字的兩項數字的比例

610÷233＝2.618025751・・・

233÷610＝0.381967213・・・

其結果就是大約是2.618和0.382。



下面是中間跳過2個數字的兩項數字的比例

610÷144＝4.236111111・・・

144÷610＝0.236065573・・・

其結果就是大約是4.236和0.236。所以，除了0.618和1.618以外，0.236、0.382，2.618、4.236也是斐波那契比例。

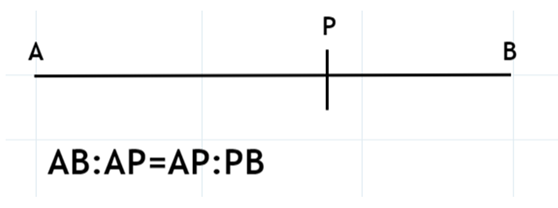
另外，0.618和1.618也被成為黃金比例。這是在1202年Leonardo Fibonacci發表斐波那契數字概念之前的西元前3世紀由歐幾里得在中末比中發現的。

圖84



閱讀全文


持有OANDA真實帳戶才可以使用OANDA獨有指標

開戶真實帳戶